Contents
Feature tracking example
This is a complete example of feature tracking on Engabreen.
- Load images & data
- Use GCPs to determine camera view direction and lens distortion parameters of image
- track stable rock features to determine camera shake and infer view direction of image B
- Pre-process DEM by filling crevasses.
- Track ice motion between images
- Georeference tracked points and calculate real world velocities.
close all
Setup file locations and load images & data
idA = 8902; idB = 8937; % image ids (/file numbers) datafolder = 'demos'; fA = fullfile(datafolder,sprintf('IMG_%4.0f.jpg',idA)); fB = fullfile(datafolder,sprintf('IMG_%4.0f.jpg',idB)); %load images: A = imread(fA); B = imread(fB); metaA = imfinfo(fA);tA = datenum(metaA.DateTime,'yyyy:mm:dd HH:MM:SS'); metaB = imfinfo(fB);tB = datenum(metaB.DateTime,'yyyy:mm:dd HH:MM:SS'); dem = load(fullfile(datafolder,'dem')); %load DEM gcpA = load(fullfile(datafolder,'gcp8902.txt'));%load ground control points for image A
Determine camera parameters for image A
- Initial crude guess at camera parameters
- Use GCPs to optimize camera parameters
%calculate focal length in pixel units: FocalLength = 30; %mm (can also be found here: metaA.DigitalCamera.FocalLength) SensorSize = [22.0 14.7]; %mm: http://www.cnet.com/products/canon-eos-rebel-t3/specs/ imgsz = size(A); f = imgsz([2 1]).*(FocalLength./SensorSize); %known camera location: cameralocation = [446722.0 7396671.0 770.0]; %crude estimate of look direction. camA = camera(cameralocation,size(A),[200 0 0]*pi/180,f); %loooking west %Use GCPs to optimize the following camera parameters: %view dir, focal lengths, and a simple radial distortion model [camA,rmse,aic] = camA.optimizecam(gcpA(:,1:3),gcpA(:,4:5),'00000111110010000000'); fprintf('reprojectionerror = %3.1fpx AIC:%4.0f\n',rmse,aic) %Visually compare the projection of the GCPs with the pixel coords: figure axes('position',[0 .1 1 .8]); hold on image(A) axis equal off ij tight hold on uv = camA.project(gcpA(:,1:3)); h = plot(gcpA(:,4),gcpA(:,5),'+',uv(:,1),uv(:,2),'rx'); legend(h,'UV of GCP','projection of GCPs','location','southoutside') title(sprintf('Projection of ground control points. RMSE = %.1fpx',rmse))
reprojectionerror = 5.1px AIC: 155

Determine view direction of camera B.
- find movement of rock features between images A and B
- determine camera B by pertubing viewdir of camera A.
% First get an approximate estimate of the image shift using a single large % template [duoffset,dvoffset] = templatematch(A,B,3000,995,'templatewidth',261,'searchwidth',400,'supersample',0.5,'showprogress',false) % Get a whole bunch of image shift estimates using a grid of probe points. % Having multiple shift estimates will allow us to determine camera % rotation. [pu,pv] = meshgrid(200:700:4000,100:400:1000); pu = pu(:); pv = pv(:)+pu/10; [du,dv,C] = templatematch(A,B,pu,pv,'templatewidth',61,'searchwidth',81,'supersample',3,'initialdu',duoffset,'initialdv',dvoffset); % Determine camera rotation between A and B from the set of image % shifts. % find 3d coords consistent with the 2d pixel coords in points. xyz = camA.invproject([pu pv]); % the projection of xyz has to match the shifted coords in points+dxy: [camB,rmse] = camA.optimizecam(xyz,[pu+du pv+dv],'00000111000000000000'); %optimize 3 view direction angles to determine camera B. rmse %quantify the shift between A and B in terms of an delta angle. DeltaViewDirection = (camB.viewdir-camA.viewdir)*180/pi
duoffset =
13.679
dvoffset =
-1.244
rmse =
0.4059
DeltaViewDirection =
0.12633 0.017584 0.015242
Generate a set of points to be tracked between images
- Generate a regular grid of candidate points in world coordinates.
- Cull the set of candidate points to those that are visible and glaciated
% The viewshed is all the points of the dem that are visible from the % camera location. They may not be in the field of view of the lens. dem.visible = voxelviewshed(dem.X,dem.Y,dem.filled,camA.xyz); %Make a regular 50 m grid of points we would like to track from image A [XA,YA] = meshgrid(min(dem.x):50:max(dem.x),min(dem.y):50:max(dem.y)); ZA = interp2(dem.X,dem.Y,dem.filled,XA,YA); %Figure out which pixel coordinates they correspond to: [uvA,~,inframe] = camA.project([XA(:) YA(:) ZA(:)]); %where would the candidate points be in image A %Insert nans where we do not want to track: keepers = double(dem.visible&dem.mask); %visible & glaciated dem points keepers = filter2(ones(11)/(11^2),keepers); %throw away points close to the edge of visibility keepers = interp2(dem.X,dem.Y,keepers,X(:),Y(:))>.99; %which candidate points fullfill the criteria. uvA(~(keepers&inframe)) = nan;
Track points between images.
% calculate where points would be in image B if no ice motion % ( i.e. accounting only for camera shake) camshake = camB.project(camA.invproject(uvA))-uvA; options = []; options.pu = uvA(:,1); options.pv = uvA(:,2); options.method = 'OC'; options.showprogress = true; options.searchwidth = 81; options.templatewidth = 21; options.supersample = 2; %supersample the input images for better subpixel estimation options.initialdu = camshake(:,1); options.initialdv = camshake(:,2); [du,dv,C,Cnoise] = templatematch(A,B,options); uvB = uvA+[du dv]; signal2noise = C./Cnoise;
Georeference tracked points
... and calculate velocities
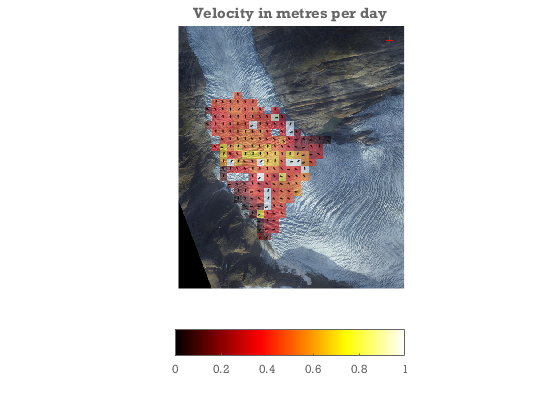
xyzA = camA.invproject(uvA,dem.X,dem.Y,dem.filled); % has to be recalculated because uvA has been rounded. xyzB = camB.invproject(uvB,dem.X,dem.Y,dem.filled-dem.mask*22.75*(tB-tA)/365); % impose a thinning of the DEM of 23m/yr between images. V = (xyzB-xyzA)./(tB-tA); % 3d velocity. Vx = reshape(V(:,1),size(XA)); Vy = reshape(V(:,2),size(YA)); Vz = reshape(V(:,3),size(ZA)); figure; showimg(dem.x,dem.y,dem.rgb); hold on Vn = sqrt(sum(V(:,1:2).^2,2)); keep = signal2noise>2 & C>.7; alphawarp(XA,YA,sqrt(Vx.^2+Vy.^2)) quiver(xyzA(keep,1),xyzA(keep,2),V(keep,1)./Vn(keep),V(keep,2)./Vn(keep),.2,'k') caxis([0 1]) colormap hot hcb = colorbar('southoutside'); plot(camA.xyz(1),camA.xyz(2),'r+') title('Velocity in metres per day')
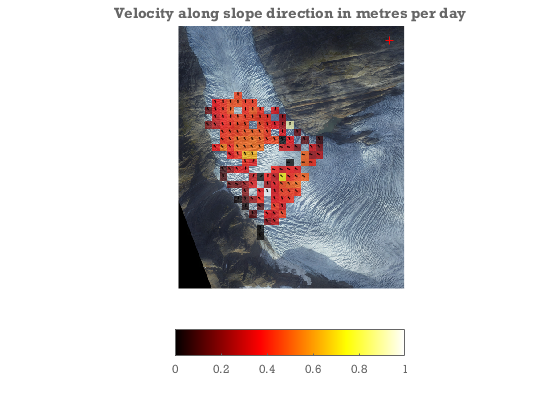
Project velocity onto downhill slope direction
---- The largest error in the velocities will along the view direction vector. By projecting to the slope direction we strongly suppress errors arising from this.
[gradX,gradY] = gradient(dem.filled,dem.X(2,2)-dem.X(1,1),dem.Y(2,2)-dem.Y(1,1)); gradN = sqrt(gradX.^2+gradY.^2); gradX = -gradX./gradN;gradY = -gradY./gradN; gradX = interp2(dem.X,dem.Y,gradX,XA,YA); gradY = interp2(dem.X,dem.Y,gradY,XA,YA); Vgn = Vx.*gradX+Vy.*gradY;%Velocity along glacier Vacross = Vx.*gradY-Vy.*gradX; %Velocity across glacier keep = reshape(keep,size(XA)); %We do not trust regions with large across glacier flow. We may get large errors where the motion is %in and out of the frame. I.e. in places where the glacier surface is %viewed very obliquely. In those places we do not have a sufficiently good %view to calculate velocities. We apply a filter to remove these. keep = keep&(abs(Vgn)>abs(Vacross)); close all figure showimg(dem.x,dem.y,dem.rgb); axis equal xy off tight hold on alphawarp(XA,YA,Vgn,keep*.7) quiver(XA(keep),YA(keep),gradX(keep),gradY(keep),.2,'k') caxis([0 1]) colormap hot hcb = colorbar('southoutside'); plot(camA.xyz(1),camA.xyz(2),'r+') title('Velocity along slope direction in metres per day')